Roy again needs to travel from
(You can move the point
Roy is going to run at
What is the longest amount of time it could take Roy?
(You are given that the stationary value for total time gives a maximum.)
Express the length of arc
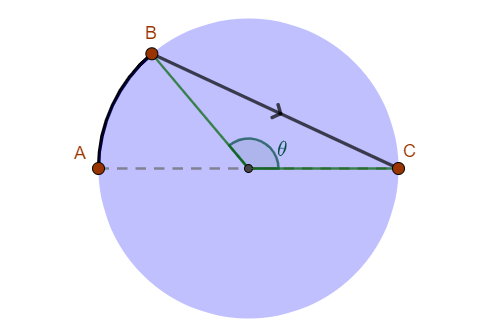
Use this to express the total time required in terms of
The graph of time against theta looks like this:
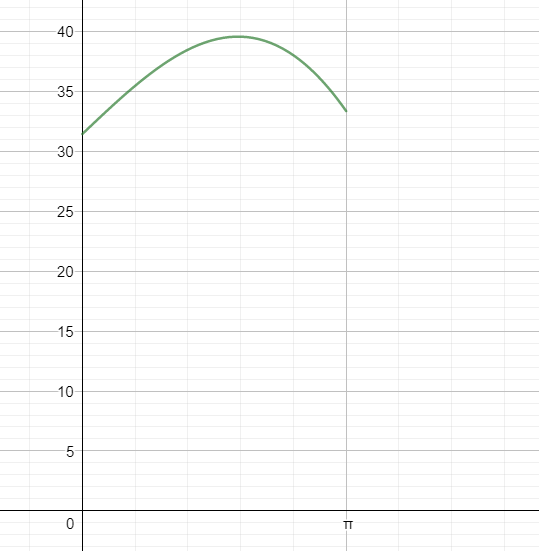
As you can see, the longest time uses a combination of running and rowing, but the quickest time does not!
Give your answer to