A cylinder of radius $2\text{cm}$ and length $10\text{cm}$ is formed from a metal alloy. The density, $\rho ,$ of the cylinder changes along the length of the rod according to the function

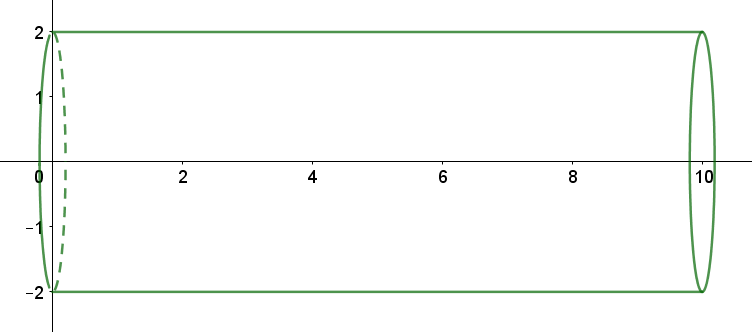
A researcher needs a quick estimate for the mass of the rod, and so he splits the rod into $5$ sections of equal width and assumes the density is constant along each section, where the density of the first section is assumed to be $\rho (0)$, and so on.

1. By forming a Riemann sum, calculate the researcher's estimate.

2. By sketching $\rho (x),$ explain whether this is an overestimate or an underestimate.

3. Describe how the estimate might be improved.

4. Write an expression using $\int$ notation for the actual mass of the cylinder.

Recall that

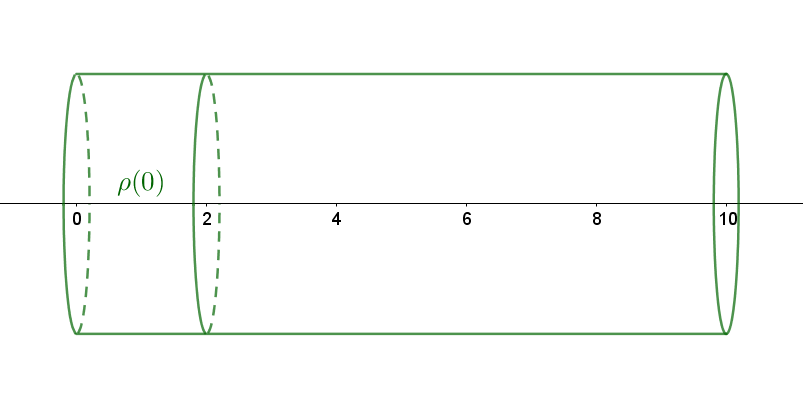
Suppose the density of the first section is $\rho (0).$ What is the volume? Therefore, what is the mass?

Do the same for the remaining sections.

Give your answer to (a), to the nearest gram.