In the previous examples, we were considering displacement as a function of time.

More generally, we can think of $y$ as a function of $x$ and consider the question

How quickly is $y$ changing as $x$ changes?

If $y=mx+c,$ then the answer is the gradient, $m,$ because increasing $x$ by $1$ will increase $y$ by $m,$ as below

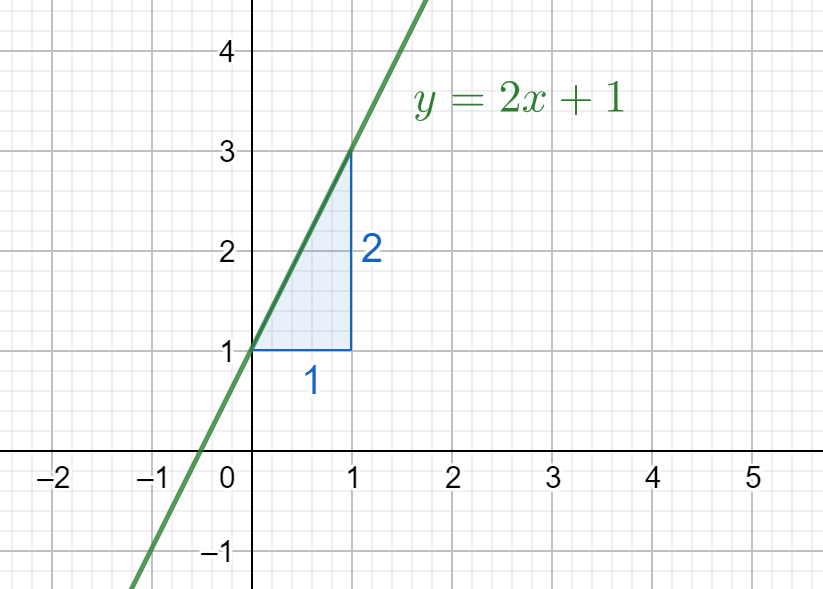
In the above picture, we would say that the rate of change of $y$ with respect to $x$ is $2.$

If $y=f(x)$ is a curve, we would find the gradient of the curve at some point $(x_0,y_0)$ by drawing a tangent to the curve, and then finding the gradient of the tangent:

You can move the point around to see how the gradient of the curve changes.

Notice that

• The gradient of the curve is larger at steeper parts of the curve

• When the curve is decreasing, the gradient is negative; when the curve is increasing, the gradient is positive

• At the minimum point, the gradient is $0$

Estimating the gradient ​

We can estimate the gradient of a curve at a given point by drawing a secant line.

A secant line is a line that passes through two points on the curve that are close together. If the points are close enough, the gradient of the secant is nearly equal to the gradient of the tangent:

Go ahead and move the point $Q$ closer to the point $P$ and observe how the secant and tangent converge together.

The actual gradient of the tangent is given the notation

so, when $Q$ is close to $P,$ we can say that

A curve is given by

By considering the secant over an $x$-interval of width $0.1,$ estimate the gradient of this curve at the point on the curve where $x=\frac{\pi }{3}.$