At a local maximum point or a local minimum point, the gradient satisfies

You can see this geometrically because the tangent is horizontal:

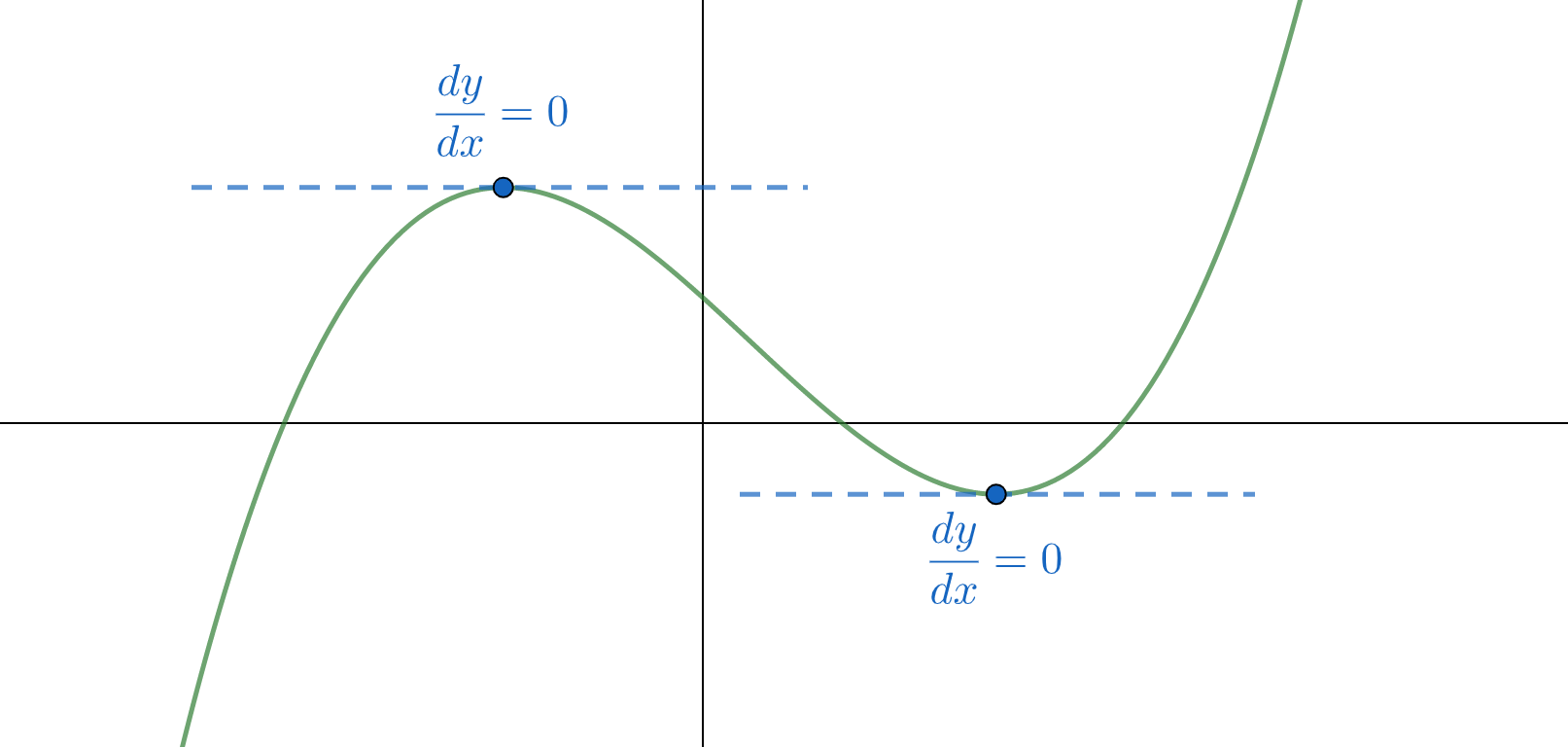
Thus, in order to find these maximum and minimum points, we can solve the equation

Collectively, maxima and minima are known as turning points.

Classifying turning points ​

Once we have found a turning point, how should we decide if it is a maximum or a minimum turning point?

To do this, we consider whether the gradient of the curve is increasing:

To do this, we must consider the rate of change of the gradient function, $\frac{dy}{dx}.$ When we differentiate $\frac{dy}{dx}$ we find the second derivative of $y$. We have the following special notation:

The reason we write $\frac{d^{2}y}{d{x}^2}$ is because we are finding

The second derivative test ​

If $\frac{dy}{dx}=0$ and

• $\frac{d^{2}y}{d{x}^2}>0$ then the gradient is increasing, so we have a minimum point: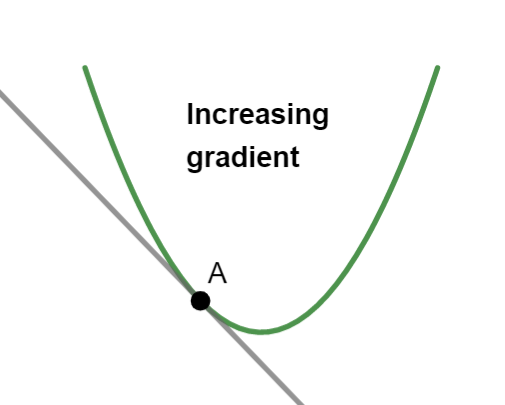

• $\frac{d^{2}y}{d{x}^2}<0$ then the gradient is decreasing, so we have a maximum point: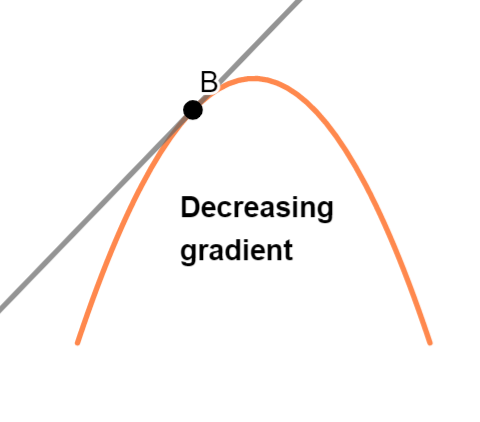

Let's try it out!

Find the turning points of the curve

and determine the nature of the turning points.