Consider again the problem of finding the area

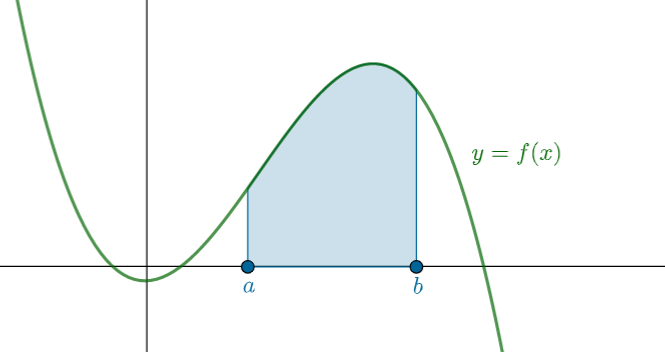
We've seen how we can do this with the trapezium rule, and Riemann sums are another way. In some ways, a Riemann sum is just a much simpler cousin of the trapezium rule. Instead of trapezia, we use rectangles:

Nevertheless, if we keep adding more and more rectangles, the Riemann sum converges to the true area just as surely as the trapeziums would. Slide $n$ in the image above to see what happens as $n$ (the number of rectangles) becomes large.

Let's take a closer look at a rectangle

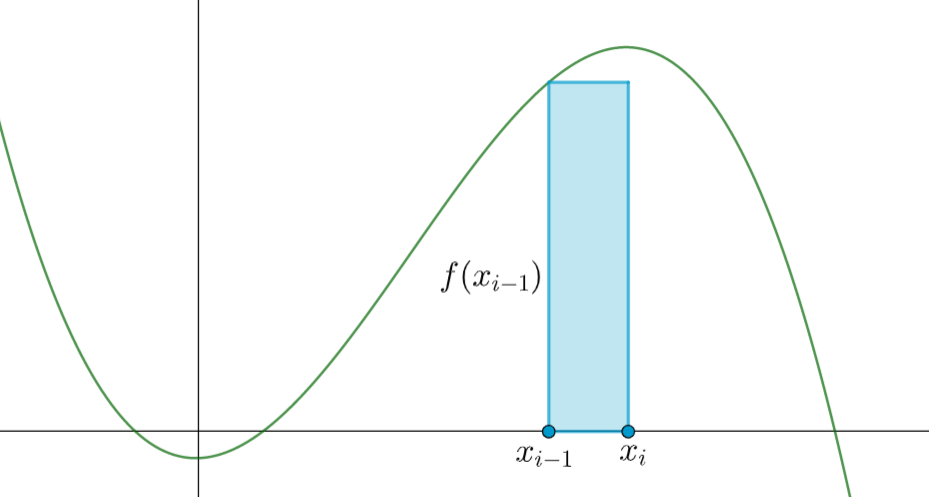
We see its area is

We often write $\mathrm{\Delta }x=x_i-x_{i-1}$ for ease. When we add all the rectangles together, we get an approximation for the area:

As we add more and more rectangles, this approximation becomes more and more accurate. In fact

So this explains the notation: $\int$ is the area after the $\sum$ of rectangles has been smoothed out, and since the rectangles become very thin, the large $\mathrm{\Delta }x$ becomes the small $dx$

Let

Given the below table of values

calculate a $4$-rectangle Riemann sum estimate for