The trapezium rule

Consider the area of the shape below:

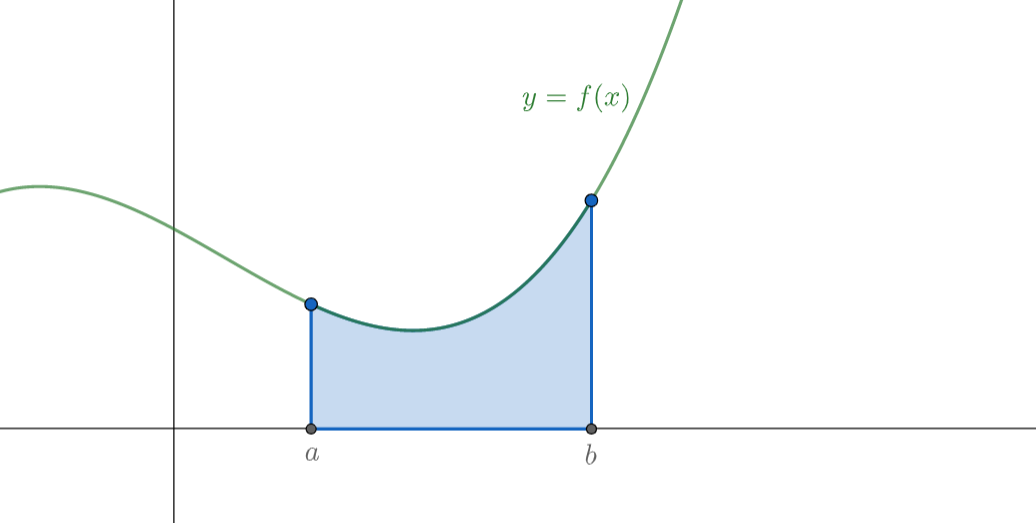
This area is bound between

the line $x = a$
the line $x = b$
the line $y = 0$ (the $x$ axis)
the curve $y = f (x)$

For this area, we use the special notation

Area = \int_{a}^{b} f (x) d x

This notation tells use where the area starts ( $x = a$ ), where the area stops ( $x = b$ ), and the function $f (x)$ which gives the curve. There are various methods for calculating exactly the area $\int_{a}^{b} f (x) d x$ which we will learn in the next chapter, but in this tutorial we will learn how to approximate areas like this using trapeziums.

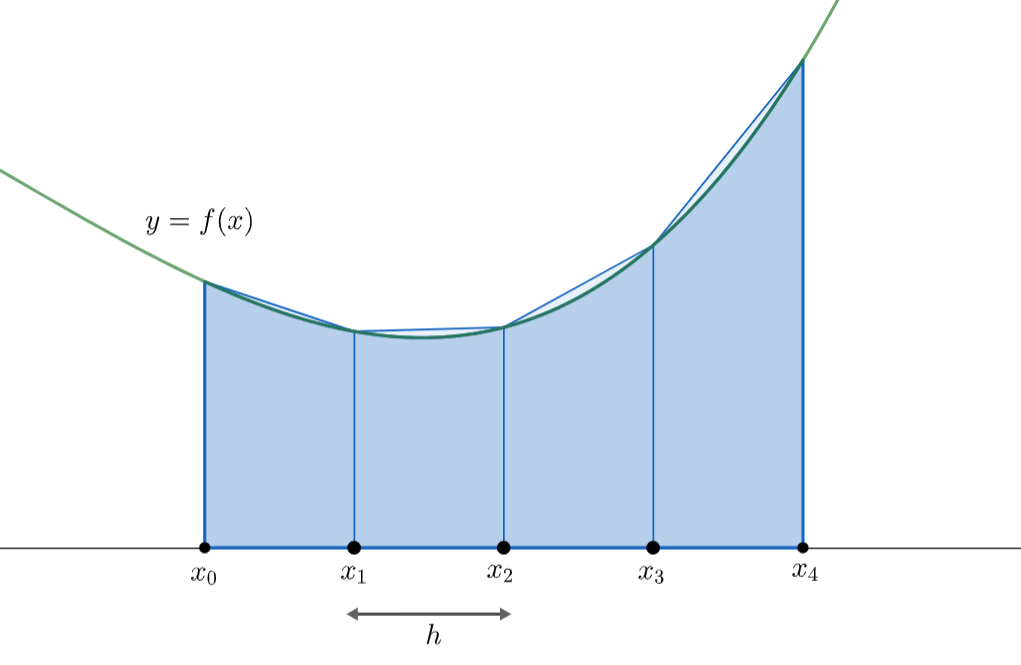
In the image below, we show how $4$ trapezia can be used to estimate the area under the curve (note that we have let $a = x_{0}$ and $b = x_{4}$ ).

The base of each trapezium is $h,$ and if the trapezia all have the same width then

h = \frac{b - a}{4}

Let's take a look at one of these trapezia

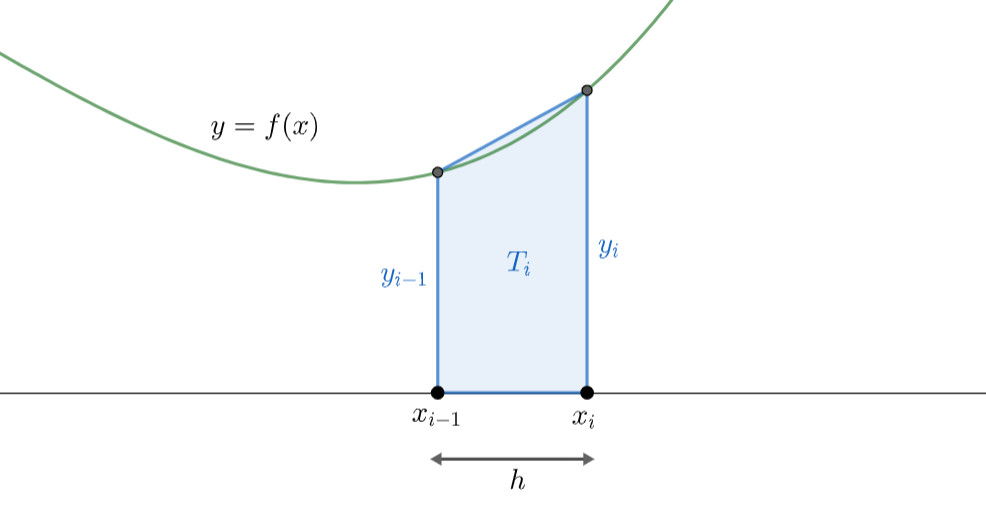
The area of the trapzium is

T_{i} = \frac{h}{2} (y_{i - 1} + y_{i})

and so the whole area can be approximated by

\begin{aligned} \int_{a}^{b} f (x) d x & \approx T_{1} + T_{2} + T_{3} + T_{4} \\ = \frac{h}{2} (y_{0} + y_{1}) + \frac{h}{2} (y_{1} + y_{2}) + \frac{h}{2} (y_{2} + y_{3}) + \frac{h}{2} (y_{3} + y_{4}) \\ = \frac{h}{2} {y_{0} + y_{1} + y_{1} + y_{2} + y_{2} + y_{3} + y_{3} + y_{4}} \\ = \frac{h}{2} {y_{0} + y_{4} + 2 (y_{1} + y_{2} + y_{3})} \end{aligned}

This last line is the most convenient form of the trapezium rule.

More generally, using $n$ trapezia we get

\int_{a}^{b} f (x) d x \approx \frac{h}{2} {y_{0} + y_{n} + 2 (y_{1} + y_{2} + \dots + y_{n - 1})}

where

h = \frac{b - a}{n}

Let's see how to use this in practice.

Using the trapezium rule with $5$ strips ( $6$ ordinates), find an estimate for the area

\int_{1}^{2} x^{2} + 1 d x

giving your answer to $3$ significant figures.

The trapezium rule ​

The trapezium rule